| Szerző: Sárneczky Krisztián | 2013. június 27., csütörtök |
|
Másfél évtizednyi intenzív kutatómunka után június 18-án felfedezték a tízezredik földsúroló kisbolygót, ám megpihenni nem lehet, még legalább tízszer ennyit kell találni ahhoz, hogy a veszélyes becsapódásokat biztosan előre tudjuk jelezni.
A június 18-án felfedezett 2013 MZ5 jelű földközeli kisbolygó teljesen átlagos égitestnek számít az évente újonnan talált nagyjából ezer földközeli objektum között. Az egyetlen, amiért nevezetessé vált, hogy ő a tízezredik. A Hawaii-szigeteken található Haleakala vulkán kihűlt kráterében felépített 1,8 méteres Pan-STARSS-1 teleszkóppal fedezték fel, fényessége 20,5-21 magnitúdó volt, átmérője 300 méter körüli, 1,277 CSE-re közelíti meg a Napot, vagyis a bolygónkra közvetlen veszélyt nem jelent. Mégis számon tartják, ahogy minden olyan égitestet a Naprendszerben, amely 1,3 CSE-nél jobban megközelíti csillagunkat, mert ha az adott pillanatban nem is, de a jövőben valamikor ezek az égitestek válhatnak potenciálisan veszélyes kisbolygóvá. Ez utóbbiak egyébként azok, amelyek 0,05 CSE-nél (7,5 millió km) jobban megközelítik a Földet, és átmérőjük meghaladja a 140 métert. Talán ezekre érdemes használni a magyarban meghonosodott földsúroló elnevezést, a többiek pedig inkább földközeli égitestek.
A 2013 MZ5 felfedező felvételeiből készített animáció. A négy képből készült mozgófilmen a jobb felső sarokból halad a bal alsó felé a gyors mozgása miatt kicsit elhúzódó nyomot hagyó kisbolygó. (PS-1/UH) Az első földközeli kisbolygót, az Eros-t 1898-ban fedezték fel, de még az 1960-as években is különleges ritkaságnak gondolták a bolygónkat megközelítő aszteroidákat. Az 1970-es években kezdett megváltozni a helyzet, mikor néhány állhatatos kutató (Tom Gehrels, Eugene Shoemaker, Eleanor Helin) munkája nyomán egyre több ilyen égitestet fedeztek fel, majd a következő évtizedben már teljesen egyértelmű volt, hogy manapság is igen nagy számban keringenek veszélyes apróságok a Naprendszerben. Az 1 km-nél nagyobbak intenzív felkutatása 1998-ban vette kezdetét, amikor a NASA jelentős támogatása mellett tíz év alatt a nagyjából ezer ilyen méretű égitest 90%-át szerették volna megtalálni. Még mielőtt ezt sikerült volna teljesíteni (jelenleg 861-et ismerünk), 2005-ben már a 140 méternél nagyobbak kerültek célkeresztbe, melyekből 15 ezernél is többet kell megtalálni. Jelenleg ezek 30%-a ismert, így a következő tíz évre még bőven akad tennivaló.
Az ismert földközeli kisbolygók számának gyarapodása 1980 óta. A végleges megnyugvást a 30 méternél nagyobbak megismerése jelenthetné, ezekből viszont már 1 milliónál is több lehet, így vélhetően a mostani kisiskolásokból is válhat még kisbolygóvadász, ha egyetemi éveik után csatlakoznak valamelyik jövőbeni keresőprogramhoz. Addig viszont úgy kell tekintenünk a földközeli kisbolygókra, mint a természet azon szeszélyére – a földrengések, vulkánkitörések vagy áradások mellett –, melyek részei az életünknek, ám ellentétben az imént felsoroltakkal, megismerésük után pontosan előrejelezhetők és elháríthatók lesznek.
|
FIZIKA :
Relativitáselmélet

Speciális relativitáselmélet[]
Az 1905-ben kiadott speciális relativitáselmélet csak azokkal a megfigyelőkkel foglalkozik, akik egymáshoz képest egyenletesen mozgó speciális rendszerben, úgynevezett inerciarendszerbenhelyezkednek el. Einstein írása, amely akkor megjelent: „A mozgó testek elektrodinamikájáról” címet viselte, később kapta az elmélet a speciális relativitáselmélet nevet. A relativitást ez az írás az idő, atér, a tömeg és az energia elméleteként vezeti be. Az elmélet felteszi, hogy a fénysebességvákuumban ugyanaz minden megfigyelő számára. A speciális relativitáselmélet megoldja a problémát, mely a Michelson-Morley kísérlet óta áll fenn, mivel nem sikerült kimutatni, hogy a fény valamilyen közegben (éterben) mozogna (minden egyéb hullám közegben mozog, például vízben vagy levegőben). Megoldja a klasszikus mechanika és a Maxwell-elmélet közötti ellentmondást is: az első szerint a fénnyel szemben haladva nagyobbnak kell mérnem a sebességét, a második szerint ugyanakkora minden rendszerben. Az elmélet rögzítette, hogy nincs ilyen közeg: a fénysebesség minden megfigyelő számára állandó, nem függ a megfigyelő mozgásától. A newtoni mechanikában ez nem lehetséges, így Einsteinnek egy új rendszert kellett kidolgoznia.
Egyik következménye a hosszúság-kontrakció, melynek értelmében egy nyugvó rendszerben l hosszúságú test egy mozgó koordináta-rendszerben megrövidül, hosszúsága az eredeti hosszúság  -szorosa lesz. Ez a jelenség hosszúságmérő eszközökkel nem bizonyítható, mivel azok is hosszúság-kontrakciót szenvednek.
-szorosa lesz. Ez a jelenség hosszúságmérő eszközökkel nem bizonyítható, mivel azok is hosszúság-kontrakciót szenvednek.
Egy másik következmény az idődilatáció, mely szerint egy nyugvó rendszerben Δt idő alatt lejátszódó esemény egy mozgó koordináta-rendszerben hosszabb ideig tart:
Az idődilatáció és a hosszúság-kontrakció egymásból következő fogalom, a kísérleti bizonyítékok csak a kettő együttes feltevése esetén állják meg a helyüket. A legismertebb bizonyíték a kozmikusmüonok bomlása. E szerint a természetben nyugalmi rendszerben 2·10−6 másodperc bomlásidejű müonok, amelyek a sztratoszférában keletkeznek, megfigyelhetőek a földfelszínen, mivel azok koordináta-rendszerében „lassabban telik az idő”, illetve „rövidebb távolságot kell megtenni”, így képes a mintegy 30 km-es útján végigmenni, és leérkezni a Föld felszínére.
Általános relativitáselmélet[]
Az általános relativitáselméletet Einstein 1916-ban publikálta (1915. november 25-énelőadássorozatban adta elő a Porosz Tudományos Akadémián). Megemlítendő, hogy a kovariáns egyenleteket Einstein előtt már David Hilbert felírta és publikálta, mégsem vádolhatjuk Einsteint utánzással. Inkább arról van szó, hogy ők ketten együtt alkották meg az általános relativitáselméletet. Az elmélet bevezet egy egyenletet, amely helyettesíti a Newtoni gravitációt. Ez felhasználja a matematikából a differenciálgeometriát és a tenzorokat, hogy leírja a gravitációt.
Ez az elmélet minden megfigyelőt egyenértékűnek tekint, nem csak azokat, akik egyenletes sebességgel mozognak. Az általános relativitás érvényes azokra is, akik egymáshoz képest gyorsulva mozognak. Ebben az elméletben a gravitáció nem egy erő többé (amilyen Newton gravitációelméletében volt), hanem a tér-idő görbületének következménye. Az általános relativitáselmélet egy geometriai elmélet, mely szerint a tömeg és az energia (pontosabban azenergia-impulzus tenzor) „meggörbíti” a téridőt, és a görbület hatással van a szabad részecskék mozgására, sőt még a fényére is. Az elmélet felhasználható a Világegyetem fejlődésével kapcsolatos modellek felállítására, és így a kozmológia alapvető eszköze. Ez az elmélet jelenti az alapját akozmológia standard modelljének, és ez ad eszközt ahhoz, hogy megértsük a Világegyetem tulajdonságait, azokat a tulajdonságokat, amelyeket csak jóval Einstein halála után fedeztek fel.
Konkurens elmélet: a Lorentz-elv[]
A speciális relativitás-elmélettel lényegében egy időben jelent meg a Lorentz-elv, amely az Einstein-féle speciális relativitás-elmélettel matematikailag teljesen ekvivalens, filozófiai szempontból ugyanazon formalizmus más interpretációját adja. A fő különbség, hogy Lorentz szerint minden test gyorsítás következményeképp valódi, fizikai deformációt szenved, így méterrúdjaink is. A fény sebessége csak egyetlen kitüntetett vonatkoztatási rendszerben izotróp, de minden más rendszerben is annak tűnik a kontrakció és idődilatáció kompenzáló hatásai miatt. Empirikusan nem lehet különbséget tenni a két elmélet között, bizonyos szempontból, a newtoni fizikán nevelkedett agy számára természetesebb a Lorentz-elv, például nem kell feladni az egyidejűség elvét, a fény sebessége valóban változik a vonatkoztatási rendszertől függően. A Lorentz-elvvel szemben az Einstein-féle felfogás terjedt el és vált elfogadottá, mivel a tudomány két ekvivalens elmélet közül a kevesebb és egyszerűbb alapfeltevésből kiindulót preferálja (Occam borotvája). Einstein elméletének nincs szüksége az éter fogalmára, és a Lorentz-transzformáció képleteit általánosabb elvekbőllevezeti, és nem posztulálja.
Az elméletet Jánossy Lajos fejlesztette tovább, aki filozófiai, világnézeti alapból preferálta a Lorentz-féle nézetet az einsteini szemlélettel szemben.[1]
Kvantummechanika
Elméletek[]
Számos kvantumgravitációval kapcsolatos elmélet létezik:
kvantumállapot · szuperpozíció · interferencia ·összefonódás · mérés · határozatlanság · Pauli-elv ·hullám-részecske kettősség · dekoherencia

kétrés-kísérlet · Davisson–Germer-kísérlet · Stern–Gerlach-kísérlet · Bell-egyenlőtlenség · Popper-kísérlet ·Schrödinger macskája · Compton-szórás
Kvantumtérelmélet · Wightman axiómái · Kvantum-elektrodinamika · Kvantum-színdinamika ·Kvantumgravitáció · Feynman-gráf
Koppenhágai · Ensemble · Rejtett változók ·Transactional · Sok-világ · Consistent histories ·Kvantumlogika · Az (ön)tudatosság eredménye összeesés
Planck · Schrödinger · Heisenberg · Bohr · Pauli · Dirac ·Bohm · Born · de Broglie · Neumann · Einstein ·Feynman · Everett · Penrose · Stephen Hawking ·Továbbiak
Húrelmélet
A húrelmélet és az M-elmélet két egymásra épülőrészecskefizikai modell, mely a részecskéket nem pontszerű, hanem kiterjedt objektumokként kezeli (húrok, membránok). A húrelméletnek a szuperszimmetriát is tartalmazó változatát gyakran szuperhúrelméletnek nevezik. Ezeket az elméleteket azért hozták létre, hogy azáltalános relativitáselméletet és a kvantummechanikátösszhangba hozzák, és elkerüljék a részecskefizikának azokat a buktatóit, melyek a pontszerű részecskék feltételezésével előbukkannak. Az M-elméletben nem csak húrokat, hanem membránokat és magasabb dimenziós objektumokat is feltételeznek. Jelenleg nincs semmilyen kísérleti tény, amely a húrelméletet igazolná.
A húrelmélet elnevezést mind a 26 dimenziós bozonikus húrelméletekre, mind a szuperszimmetria felfedezése után annak hozzáadásával nyert szuperhúrelméletre szokták használni. Újabban gyakran a szuperhúrelméletet mondjuk húrelméletnek. Az 1990-es években Edward Witten és mások meggyőző bizonyítékokat találtak arra, hogy a különböző szuperhúr elméletek (öt különböző változata van) egy M-elméletnek nevezett 11 dimenziós elmélet határesetei. Ezzel indult el a második szuperhúr-forradalom. (Az M-elméletnek még a feketelyukaktermodinamikájában is sikerült olyan eredményeket elérnie, amelyek a korábbi számításokkal összhangban vannak.)
A húrelmélet főként annak köszönheti népszerűségét, hogy reményeink szerint képes az összes erőhatás leírását egyetlen elméletbe összesűríteni. A húrelméletnek köszönhető, hogy mélyebben sikerült megértenünk a szuperszimmetrikus térelméleteket, amelyek a részecskéket pontszerűnek tekintő standard modellnek lehetséges kiterjesztései.
Extra dimenziók[]
A húrelmélet egyik furcsa tulajdonsága, hogy feltételezi, hogy az univerzumnak sok dimenziója van, és megjósolja a számukat. Sem Maxwell elmélete az elektromágnesességről, sem Einsteinrelativitáselmélete nem adja meg a dimenziószámot. A jól ismert 3 tér és egy idődimenziót "kézzel" helyezzük bele ezekbe az elméletekbe. Ezzel szemben a húrelméletben megjósolható a téridő dimenziószáma alapvető elvekből. (Adott dimenziószám szükséges ahhoz, hogy az elmélet Lorentz-invariáns legyen.) Az egyetlen probléma, hogyha kiszámoljuk a szükséges dimenziószámot, akkor nem négyet (3 tér + 1 idő), hanem 26-ot, 10-et illetve 11-et kapunk a bozonikus húrelméletben, a szuperhúr elméletben, illetve az M-elméletben.
Ezek a tények komolyan ellentmondanak a megfigyelt eseményeknek. A fizikusok a következő két lehetőség egyikével oldják meg a problémát. Az első módszer, ha összezsugorítjuk a hiányzó dimenziókat. Ez azt jelenti, hogy a 6 vagy 7 dimenzió olyan kicsi, hogy nem észlelhető a kísérleteinkben. A 6 dimenziós esetben ezt a Calabi-Yau terekkel oldják meg. 7 dimenzióban úgynevezett G2 manifoldokkal. Lényegében a hiányzó dimenziókat úgy teszik kicsivé, hogy azok magukba hurkolódnak. A szokásos hasonlat erre a locsolócső. Távolról nézve egydimenziós alakzatnak, vonalnak látszik, de ha közelebb megyünk, láthatóvá válik a második kiterjedése, amely kör keresztmetszetű. Ehhez hasonlóan úgy gondoljuk, hogy a hiányzó dimenziók csak közelről nézve láthatóak.
(Természetesen a locsolócső 3 dimenziós, de mi csak a felületén mozgunk. Ekkor a helyünket két számmal adhatjuk meg. Az egyik kitüntetett végétől való távolsággal és kerületén például a felső ponttól egyik kitüntetett körüljárási irányban mért távolsággal. Mivel a hely megadásához két adat kell és elegendő, ezért mondjuk, hogy a locsolócső felszíne kétdimenziós. A földfelszín is kétdimenziós, hiszen a földrajzi szélesség és hosszúság (két adat) ismeretében a hely adott.)
A másik lehetőség az, hogy mi a világegyetemnek egy 3+1 dimenziós alterében élünk, ahol a +1 emlékeztet arra, hogy az idő egy másfajta dimenzió, mint a tér. Mivel ez a látásmód D-brán nevűmatematikai objektumokkal írja le elméletét, ezért ezt bránvilág elméletnek nevezzük. Egy érdekes mellékterméke, hogy eszerint elképzelhető, hogy a kvantumgravitációs jelenségeket akár a CERN2008-ban elindult gyorsítógyűrűjében, a nagy hadronütköztetőgyűrűben (LHC) megfigyeljünk. Bár ez érdekes dolog, ebben a lehetőségben azért nem sokan hisznek.
Problémák a húrelmélettel[]
A húrelméletnek három komolyabb problémája van. Az első, hogy senki sem képes megoldani a húrok mezőelméletét, vagy hogy bármilyen más nemperturbatív eredményt hozzon ki a húrelméletből. A feladat kristálytiszta, de a sors iróniája, hogy a megoldása olyan technikákat igényel, amelyek túlmutatnak a fizikusok jelenlegi képességein. Érdekes tény, hogy miközben a huszonegyedik század fizikája véletlenül belepottyant a huszadik századba, a huszonegyedik század matematikája, még nem született meg; s már csak ezért is él ez a probléma, hogy a jelenben e húrok mezőelméletét nem tudjuk megoldani.
A második, hogy a 10-35 méter átmérőjű húrokat jelenlegi technikánkkal képtelenek vagyunk megfigyelni.
A harmadik probléma az, hogy a kvantumtérelmélethez hasonlóan csak perturbatívan kezelhető (közelítések sorozatával pontos megoldás helyett). Bár komoly előrelépések történtek a nemperturbatív módszerek felé, a teljes elmélet nem írható le ily módon.
A húrelmélet típusai[]
Öt különböző típusú húrelmélet létezik. Ezek a következőek: I típus, IIA típus, IIB típus, heterotikus-O és heterotikus-E. Ezekről sokáig azt hitték, hogy különbözőek, de a közelmúltban kiderült, hogy a húrelméletek között van összefüggés. Mert ha figyelembe vesszük a dualitást, akkor a csatolási állandók változtatása az egyik típustól elvisz a másik típusig. Így az I típusú duális a heterotikus-O-val, a heterotikus-E a IIA típusúval egyesül az M-elméleten belül, a IIB típusú pedig önmagával duális. Valamint ha figyelembe vesszük a téridő geometria dualitását is, akkor a heterotikus-O duális a heterotikus-E-vel, valamint a IIA típusú a IIB típusúval.
I típus <---> heterotikus-O
IIA típus <---> heterotikus-E
IIB típus <---> IIB típus
heterotikus-O <...> heterotikus-E
IIA típus <...> IIB típus[1]



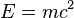 összefüggés és Einstein egy 1979-es szovjet bélyegen
összefüggés és Einstein egy 1979-es szovjet bélyegen